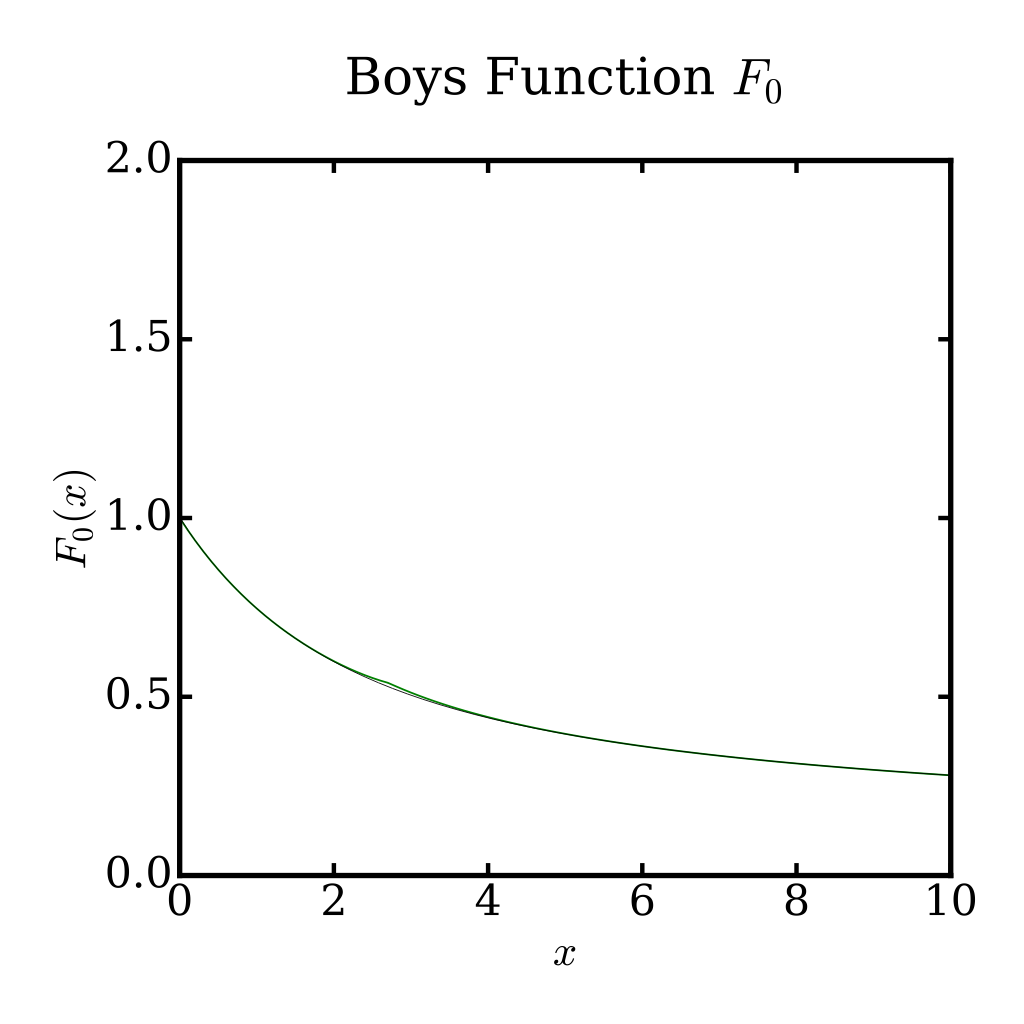
A side project that I’ve recently been working (or trying to work) on is coding a fast molecular integral library in c. An important function in the calculation of coulombic integrals is the Boys function, . This function is given by:
Evaluating this function frequently, accurately and quickly has been a focus of research for about the last half a century. I’ll present a simple example here.
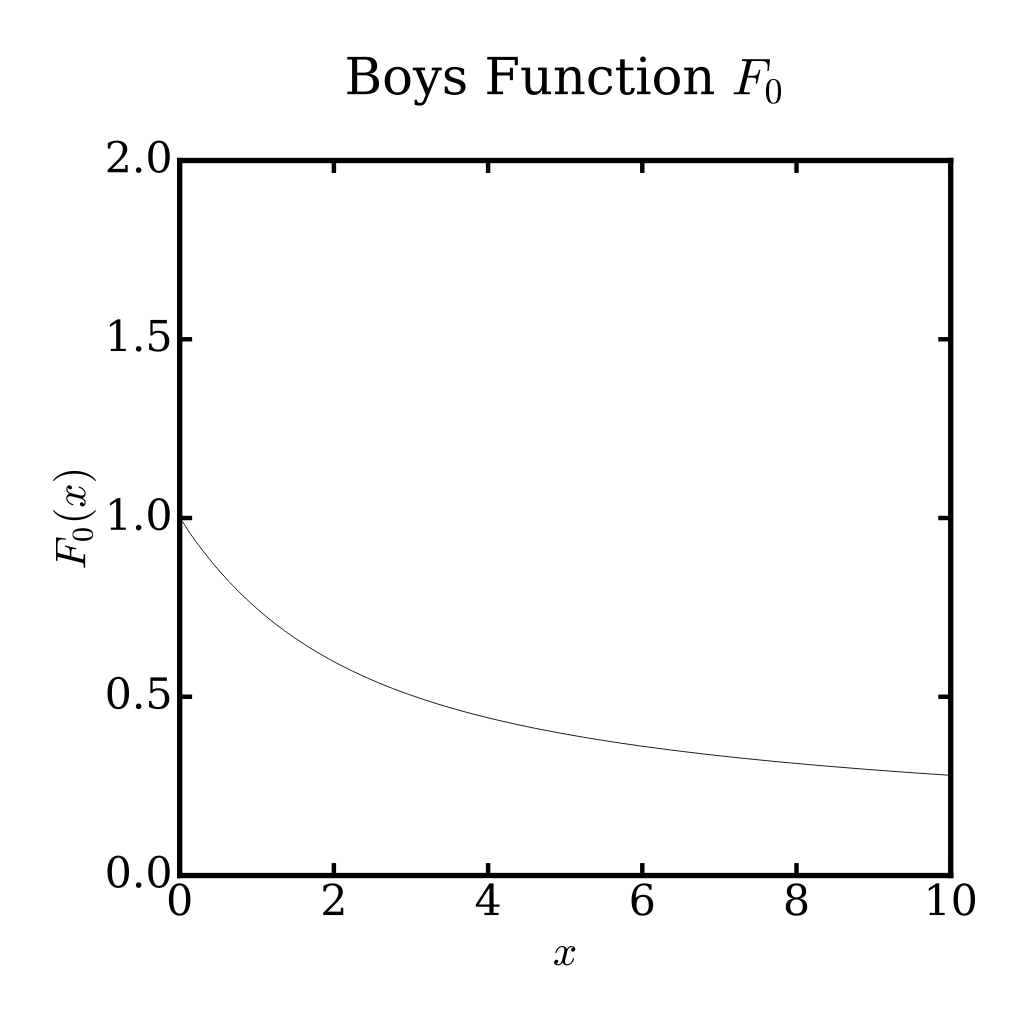
The evaluation of the Boys function can be broken into two cases, large values and small values. # Large values:
For large x values the boys function can be approximated as:
This is related to the incomplete gamma integral and can be integrated giving:
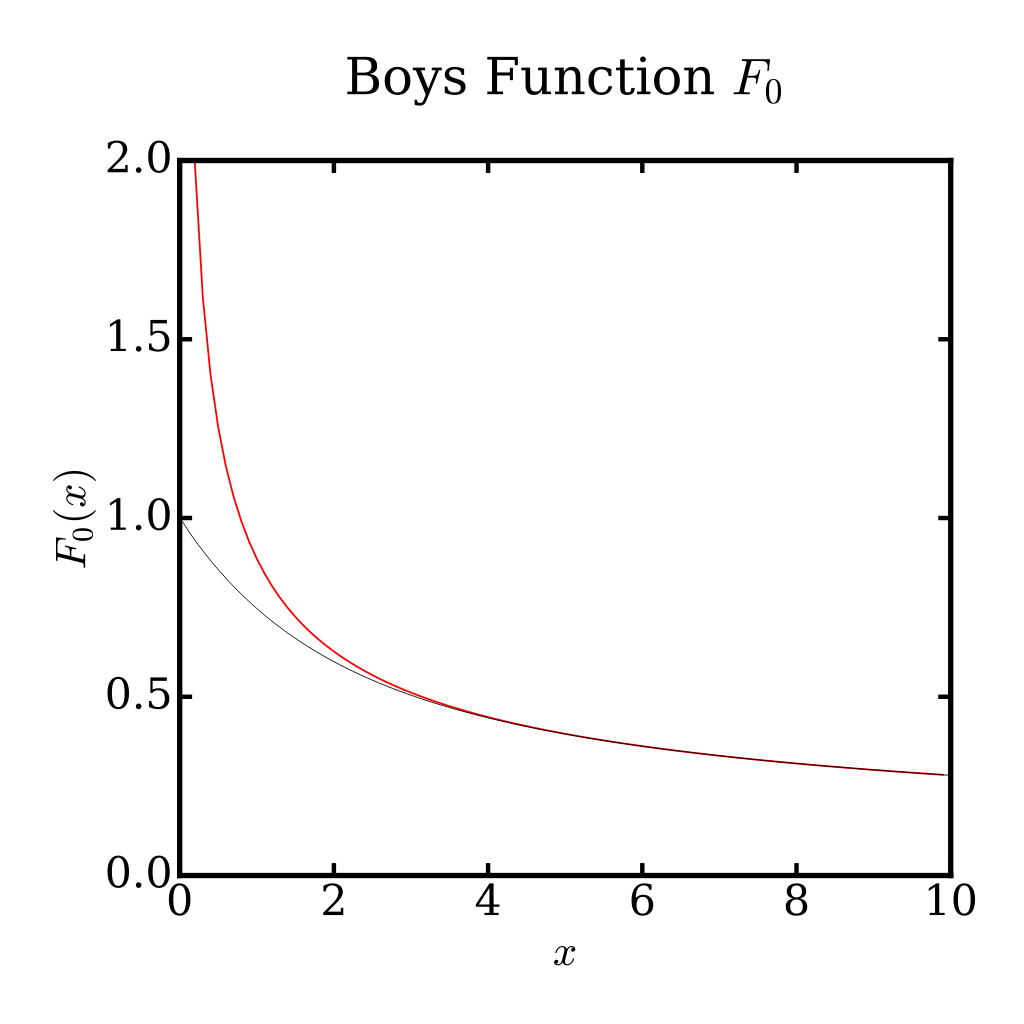
Small values:
To approximate the boys function for small values a Taylor expansion is employed:
An infinite series is impractical in application (obviously) so this is truncated to six terms to achieve reasonable accuracy in reasonable time.
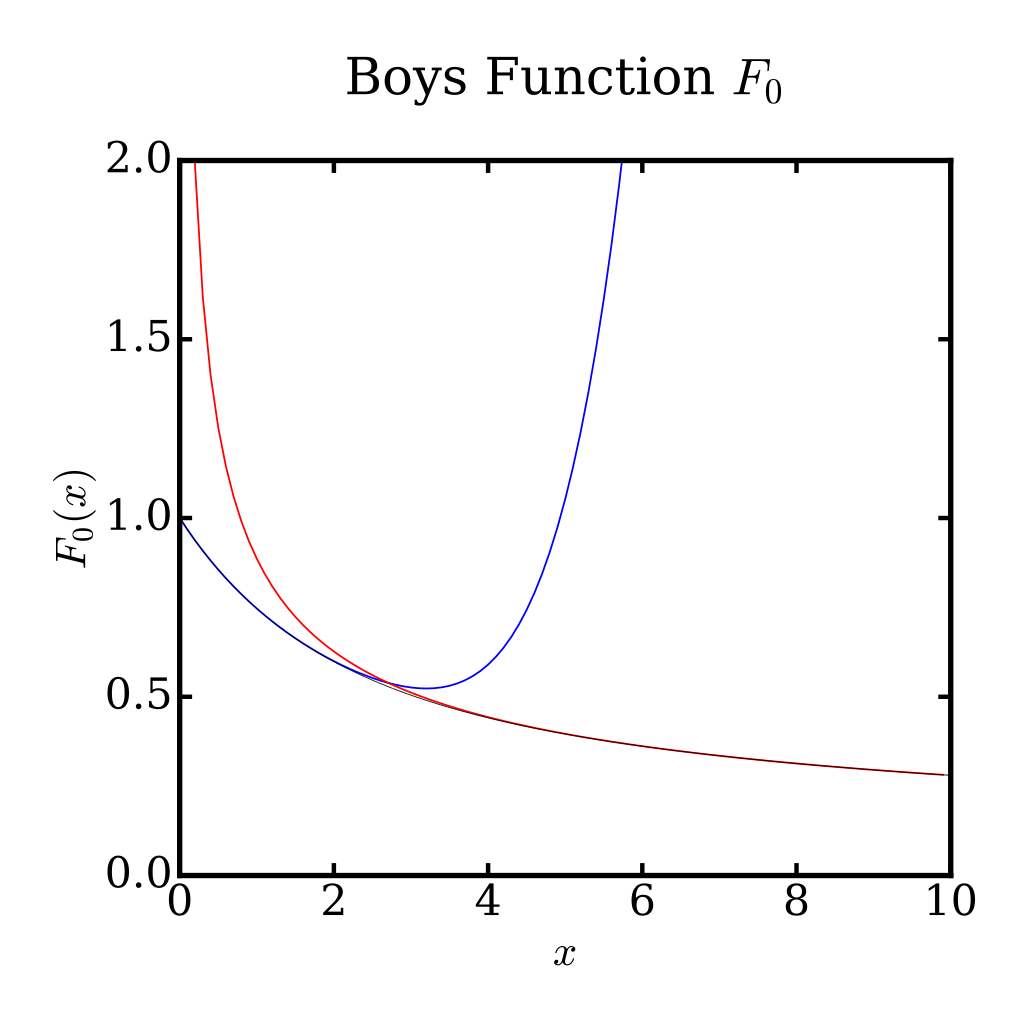
Where does become large?
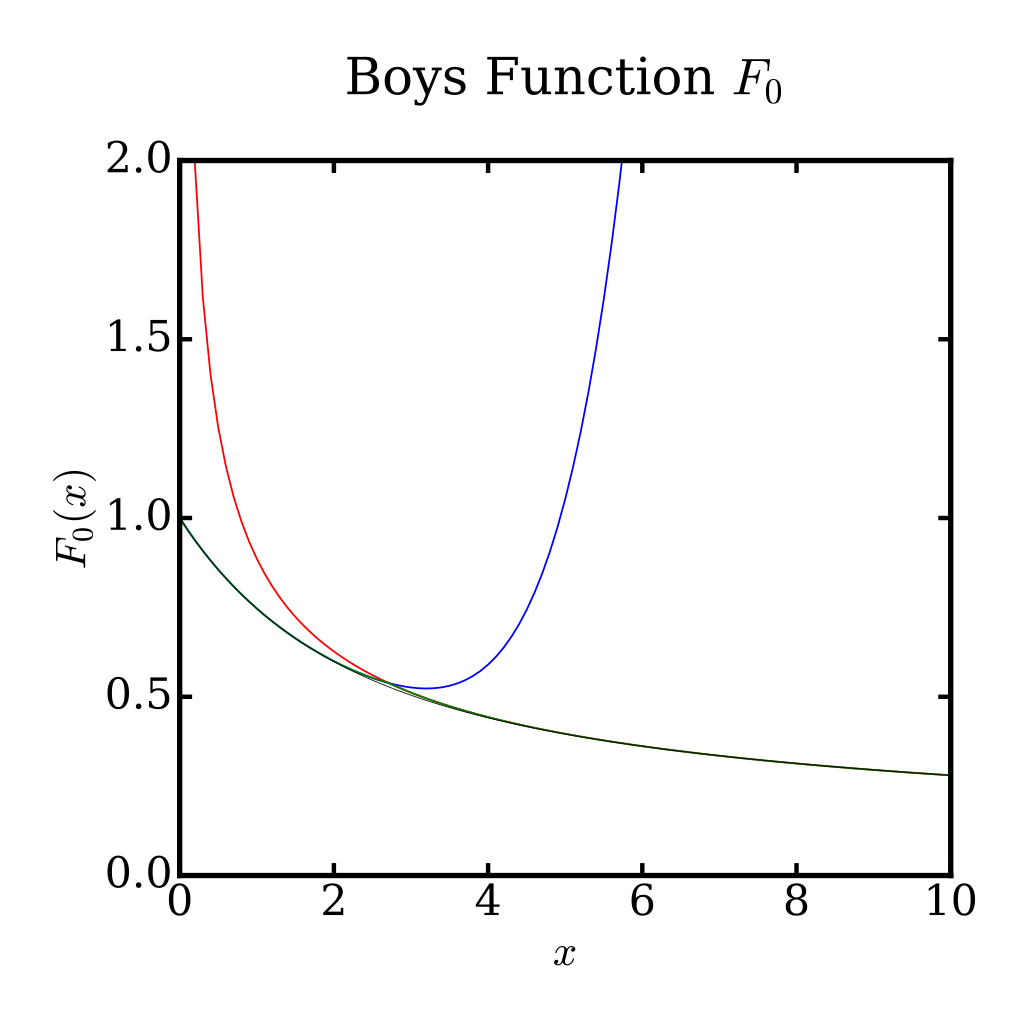
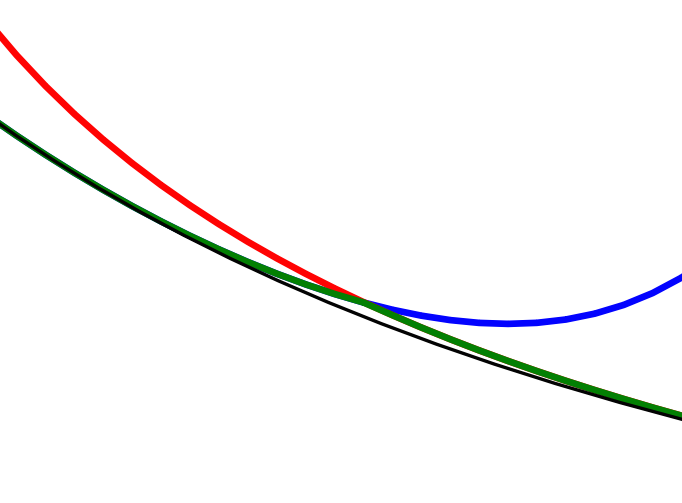
This is a question which has been bothering me, but for now I sidestepped the issue by returning the lowest value calculated by the two methods.
Potential speed ups
- I’m calculating both expressions each time which is really bad
- I’m not implementing any recursion formulas
The later point is critical what I should be doing is calculating the Boys function at a very high order on a grid of points and using a downward recursion formula (upwards recursion is numerical unstable at smal values).
References
- Molecular Electronic-Structure Theory
- Evaluation of the Boys Function using Analytical Relations
- A rigorous and optimized strategy for the evaluation of the Boys function kernel in molecular electronic structure theory
- ACE algorithm for the rapid evaluation of the electron-repulsion integral over Gaussian-type orbitals
